This post is about some former work for a seminar, I did in the third term. It’s about the problem in FEM-simulation, when you want to simulate a charge and you have neither boundary nor boundaryconditions. The solution here, formulated by Kelvin was, to separete the infinite simulationroom in an inner finite circle and an outer infinite circular disk. Once you’ve done this, you can transform the outer infinite circular disk into an finite circle of the same size of the inner one, regarding:

now you can discretisice the “infinite” circular disk in an arbitrary way but with the center as infinite and with the boundarycondition zero (with the assumption that everything dissapears in the in the infinty) .

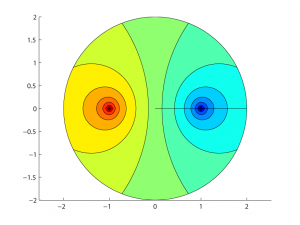
The following files may help to understand the Kelvin transformation. I also wrote an article about the FEM-simulation using finite defferences. So Enjoy reading:

Kelvin_Transfomation

Kelvin_Transfomation_Handout

Kelvin_Transformation_Praesentation

This is the MATLAB-code for the examples in the documents and of course for the Kelvin transformation

MATLAB-code

LaTeX source of the documents:

Kelvin_Transformation_Praesentation_LaTeX

Kelvin_Transfomation_Handout_LaTeX

Kelvin_Transfomation_LaTeX